PyODE Tutorial 1

By Matthias Baas.

This tutorial shows you the very basics of ODE: creating a world including a rigid body and doing a simulation loop. The example program does without any fancy graphics output, but just displays the bare numbers. Adding eye catchy 3D graphics is left as an exercise for the reader. :) So here's the entire pyODE program:

# pyODE example 1: Getting started
    
import ode

# Create a world object
world = ode.World()
world.setGravity( (0,-9.81,0) )

# Create a body inside the world
body = ode.Body(world)
M = ode.Mass()
M.setSphere(2500.0, 0.05)
M.mass = 1.0
body.setMass(M)

body.setPosition( (0,2,0) )
body.addForce( (0,200,0) )

# Do the simulation...
total_time = 0.0
dt = 0.04
while total_time<2.0:
    x,y,z = body.getPosition()
    u,v,w = body.getLinearVel()
    print "%1.2fsec: pos=(%6.3f, %6.3f, %6.3f)  vel=(%6.3f, %6.3f, %6.3f)" % \
          (total_time, x, y, z, u,v,w)
    world.step(dt)
    total_time+=dt

We'll now go through the code step by step:

import ode

The module ode contains all the classes, functions and constants from the ODE library.

# Create a world object
world = ode.World()
world.setGravity( (0,-9.81,0) )

First you have to create a World object that will hold all rigid bodies and joints and that can be used to get and set global parameters. One such parameter is the gravity which we also set here. The gravity is passed as a vector which can be any object that can be used as a 3-sequence of floats. In this case we're just using an ordinary Python tuple.

One word about units: it's not that important what kind of units you're using in ODE, you just have to be consistent. Above we've set the gravitational acceleration to -9.81 which already implies we're using the MKS system, so all lengths in this tutorial will be measured in meters, weights in kilograms and times in seconds.

# Create a body inside the world
body = ode.Body(world)
M = ode.Mass()
M.setSphere(2500.0, 0.05)
M.mass = 1.0
body.setMass(M)

For each rigid body you want to simulate you need an instance of the Body class. The most important parameters of a rigid body are its mass properties. These properties are stored in the class Mass which has the following attributes:

mass: The total mass.
c: The center of gravity.
I: The inertia tensor.

In real life these properties are determined by the geometry and density distribution of the body. For a few simple geometries and constant densities you can use methods like setSphere(), setCappedCylinder(), setCylinder() or setBox() to set the mass properties to appropriate values. To give you an idea of what numbers to use for the density parameter, the following table lists a couple of materials and their densities:

Material	Density (kg/m^3)
Balsa wood	120
Brick	2000
Copper	8900
Cork	250
Diamond	3300
Glass	2500
Gold	19300
Iron	7900
Lead	11300
Styrofoam	100

If you have to simulate more complex objects you basically have two options:

Approximate the complex object by composing several simple ones. In this case you can add the individual masses (you can actually use the + operator which will call the ODE dMassAdd() function internally).
Calculate the properties yourself and set them with Mass.setParameters(). If you're representing your objects as a polyhedron, then you might find the following paper helpful: Brian Mirtich Fast and Accurate Computation of Polyhedral Mass Properties,journal of graphics tools, volume 1, number 2, 1996

In the example program the call to M.setSphere() sets the mass properties so that the body behaves like a sphere with radius 0.05 and a constant density of 2500. You can print the mass object to see the actual values:

>>> print M
Mass=1.308996939
Cg=(0.0, 0.0, 0.0)
I11=0.001308996939 I22=0.001308996939 I33=0.001308996939
I12=0.0 I13=0.0 I23=0.0

As you can see a solid glass sphere with a radius of 5 centimeters will weigh about 1.3 kg. The next program line however will adjust the mass to 1.0 kg. This adjustment not only affects the total mass but also the inertia tensor:

>>> print M
Mass=1.0
Cg=(0.0, 0.0, 0.0)
I11=0.001 I22=0.001 I33=0.001
I12=0.0 I13=0.0 I23=0.0

You can interpret this in two ways, we either decreased the density or the radius a little bit. Whichever way you prefer to view it, the result is actually the same.

body.setPosition( (0,2,0) )
body.addForce( (0,200,0) )

Here, we adjust the initial values of the body. The first line places it at position (0,2,0) and the second will accelerate the body upwards. The force is only applied during the first computation step since these forces are automatically set to zero after each step.

# Let the sphere drop...
total_time = 0.0
dt = 0.04
while total_time<2.0:
    x,y,z = body.getPosition()
    u,v,w = body.getLinearVel()
    print "%1.2fsec: pos=(%6.3f, %6.3f, %6.3f)  vel=(%6.3f, %6.3f, %6.3f)" % \
          (total_time, x, y, z, u,v,w)
    world.step(dt)
    total_time+=dt

This is finally the simulation loop. Each call to world.step() moves all bodies inside this world. The argument to this method is the delta time to proceed. Inside the loop we retrieve the current position and linear velocity of the body and print it for further inspection.

Now let's check if these values make any sense. So what have we simulated here? We have a glass ball that weighs 1 kg which we thrust up into the air and see what happens with it.

The initial height is 2 meters above the ground and we thrust it up with a force of 200 Newton which is applied over a time interval of 0.04 seconds. Now you have to remember Newtons law F = m*a to determine the starting velocity. Since the mass is 1 kg we get an acceleration of a = 200 m/s^2. The actual acceleration, however, is 190.19 m/s^2 since we have to add the acceleration due to gravity. This acceleration is applied throughout the first simulation step, this means the velocity after that step should be v = a*t = 190.19 * 0.04 m/s = 7.608 m/s which is indeed the case (see the output of the program). After that, the only force that acts on the body is the gravity.

If you run the program you should see the following output:

0.00sec: pos=( 0.000,  2.000,  0.000)  vel=( 0.000,  0.000,  0.000)
0.04sec: pos=( 0.000,  2.304,  0.000)  vel=( 0.000,  7.608,  0.000)
0.08sec: pos=( 0.000,  2.593,  0.000)  vel=( 0.000,  7.215,  0.000)
0.12sec: pos=( 0.000,  2.866,  0.000)  vel=( 0.000,  6.823,  0.000)
0.16sec: pos=( 0.000,  3.123,  0.000)  vel=( 0.000,  6.430,  0.000)
0.20sec: pos=( 0.000,  3.365,  0.000)  vel=( 0.000,  6.038,  0.000)
0.24sec: pos=( 0.000,  3.590,  0.000)  vel=( 0.000,  5.646,  0.000)
0.28sec: pos=( 0.000,  3.801,  0.000)  vel=( 0.000,  5.253,  0.000)
0.32sec: pos=( 0.000,  3.995,  0.000)  vel=( 0.000,  4.861,  0.000)
0.36sec: pos=( 0.000,  4.174,  0.000)  vel=( 0.000,  4.468,  0.000)
0.40sec: pos=( 0.000,  4.337,  0.000)  vel=( 0.000,  4.076,  0.000)
0.44sec: pos=( 0.000,  4.484,  0.000)  vel=( 0.000,  3.684,  0.000)
0.48sec: pos=( 0.000,  4.616,  0.000)  vel=( 0.000,  3.291,  0.000)
0.52sec: pos=( 0.000,  4.732,  0.000)  vel=( 0.000,  2.899,  0.000)
0.56sec: pos=( 0.000,  4.832,  0.000)  vel=( 0.000,  2.506,  0.000)
0.60sec: pos=( 0.000,  4.916,  0.000)  vel=( 0.000,  2.114,  0.000)
0.64sec: pos=( 0.000,  4.985,  0.000)  vel=( 0.000,  1.722,  0.000)
0.68sec: pos=( 0.000,  5.039,  0.000)  vel=( 0.000,  1.329,  0.000)
0.72sec: pos=( 0.000,  5.076,  0.000)  vel=( 0.000,  0.937,  0.000)
0.76sec: pos=( 0.000,  5.098,  0.000)  vel=( 0.000,  0.544,  0.000)
0.80sec: pos=( 0.000,  5.104,  0.000)  vel=( 0.000,  0.152,  0.000)
0.84sec: pos=( 0.000,  5.094,  0.000)  vel=( 0.000, -0.240,  0.000)
0.88sec: pos=( 0.000,  5.069,  0.000)  vel=( 0.000, -0.633,  0.000)
0.92sec: pos=( 0.000,  5.028,  0.000)  vel=( 0.000, -1.025,  0.000)
0.96sec: pos=( 0.000,  4.971,  0.000)  vel=( 0.000, -1.418,  0.000)
1.00sec: pos=( 0.000,  4.899,  0.000)  vel=( 0.000, -1.810,  0.000)
1.04sec: pos=( 0.000,  4.811,  0.000)  vel=( 0.000, -2.202,  0.000)
1.08sec: pos=( 0.000,  4.707,  0.000)  vel=( 0.000, -2.595,  0.000)
1.12sec: pos=( 0.000,  4.587,  0.000)  vel=( 0.000, -2.987,  0.000)
1.16sec: pos=( 0.000,  4.452,  0.000)  vel=( 0.000, -3.380,  0.000)
1.20sec: pos=( 0.000,  4.301,  0.000)  vel=( 0.000, -3.772,  0.000)
1.24sec: pos=( 0.000,  4.135,  0.000)  vel=( 0.000, -4.164,  0.000)
1.28sec: pos=( 0.000,  3.953,  0.000)  vel=( 0.000, -4.557,  0.000)
1.32sec: pos=( 0.000,  3.755,  0.000)  vel=( 0.000, -4.949,  0.000)
1.36sec: pos=( 0.000,  3.541,  0.000)  vel=( 0.000, -5.342,  0.000)
1.40sec: pos=( 0.000,  3.312,  0.000)  vel=( 0.000, -5.734,  0.000)
1.44sec: pos=( 0.000,  3.066,  0.000)  vel=( 0.000, -6.126,  0.000)
1.48sec: pos=( 0.000,  2.806,  0.000)  vel=( 0.000, -6.519,  0.000)
1.52sec: pos=( 0.000,  2.529,  0.000)  vel=( 0.000, -6.911,  0.000)
1.56sec: pos=( 0.000,  2.237,  0.000)  vel=( 0.000, -7.304,  0.000)
1.60sec: pos=( 0.000,  1.929,  0.000)  vel=( 0.000, -7.696,  0.000)
1.64sec: pos=( 0.000,  1.606,  0.000)  vel=( 0.000, -8.088,  0.000)
1.68sec: pos=( 0.000,  1.267,  0.000)  vel=( 0.000, -8.481,  0.000)
1.72sec: pos=( 0.000,  0.912,  0.000)  vel=( 0.000, -8.873,  0.000)
1.76sec: pos=( 0.000,  0.541,  0.000)  vel=( 0.000, -9.266,  0.000)
1.80sec: pos=( 0.000,  0.155,  0.000)  vel=( 0.000, -9.658,  0.000)
1.84sec: pos=( 0.000, -0.247,  0.000)  vel=( 0.000, -10.050,  0.000)
1.88sec: pos=( 0.000, -0.665,  0.000)  vel=( 0.000, -10.443,  0.000)
1.92sec: pos=( 0.000, -1.098,  0.000)  vel=( 0.000, -10.835,  0.000)
1.96sec: pos=( 0.000, -1.548,  0.000)  vel=( 0.000, -11.228,  0.000)

Or graphically (the y position is shown in red, the velocity in green):

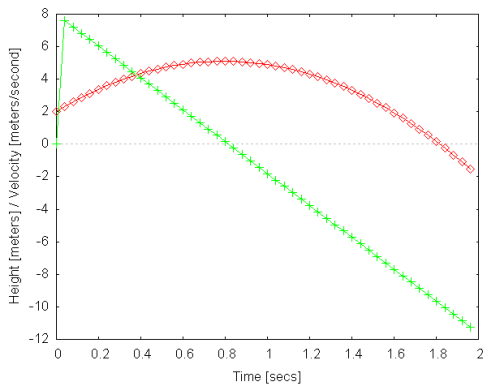
Graph showing the position and velocity curves.

Now you've seen how to create a simple simulation using the ODE library from within Python. The next steps would be to connect rigid bodies with joints and do collision detection to prevent them from interpenetrating each other. This will be covered in the following tutorials. It's also highly recommended to read the original ODE manual that explains the C API. Now that you've seen the basic usage of the Python version it should be rather straightforward to translate any C function call into the corresponding Python method call (e.g. dMassSetSphere() becomes Mass.setSphere(), etc.).